O say, can you see, by the dawn’s early light,
What so proudly we hailed at the twilight’s last gleaming?
– Francis Scott Key, Baltimore, 1814
Educator Joseph Kerski recently posted a challenge on his “Our Earth” YouTube channel. The challenge? To determine how high over Lake Michigan you need to be to see both the Wisconsin and Michigan shorelines. At its widest, the lake is 118 miles across. Do you need to be on an airplane at 37,000 feet? Or maybe just 40 feet up from the water on the deck of the SS Badger?
The Basics
To answer this challenge, I turned to some basic trigonometry. To keep this simple, let’s assume the earth is perfectly spherical, has a radius of 6,371 km (20,902,231.68 ft) and is as smooth as a ping-pong ball (no mountains, valleys, trees or buildings). Also, we are going to ignore the effects of atmospheric attenuation and refractivity – in other words, we’ll assume the atmosphere is perfectly transparent, there is no cloud, dust, smoke or haze, and there is no bending of light rays through the air.
Given these assumptions, we can compute visibility at any height as shown in Figure 1. Notice the right-angle triangle CPO. The observer – or more precisely, the observer’s eyes – are at point O, at a height of h above the earth’s surface. Point C is the center of the earth. Point P is the point where the triangle is at right angles to the earth’s surface (the point of tangency). To the observer, Point P would be on the horizon. Anything on the other side of P would not be visible.
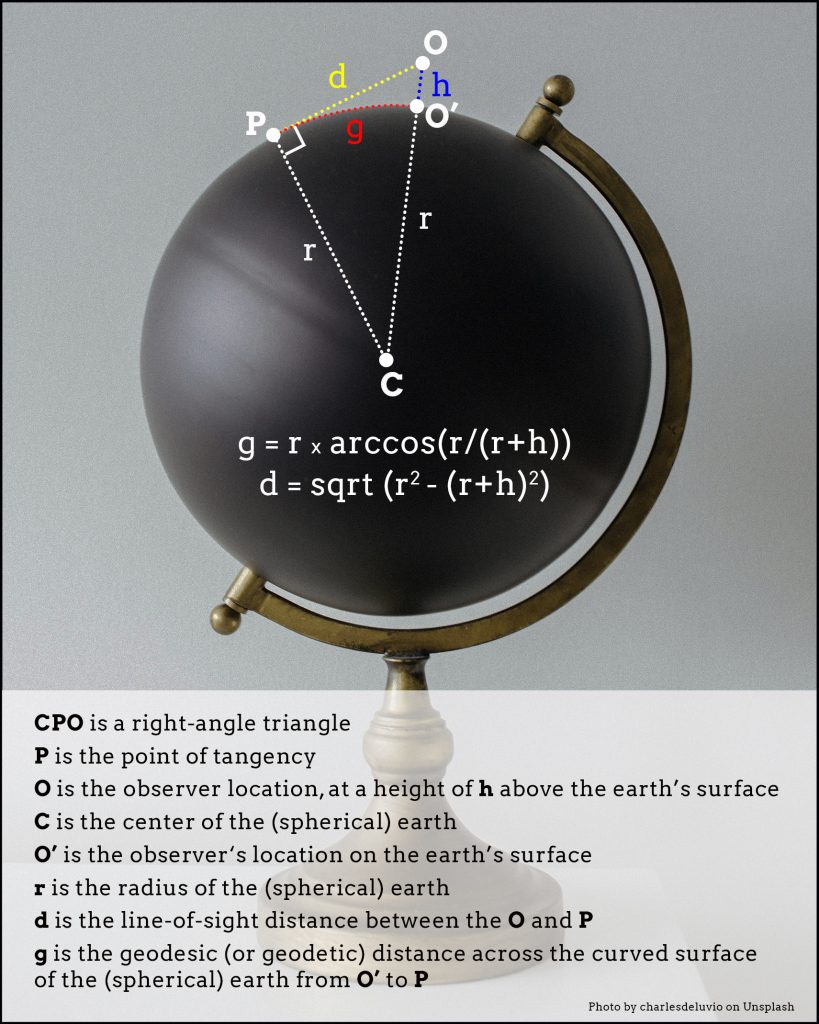
Fig. 1 – A simple solution to the Kerski Challenge
The observer’s line-of-sight distance to point P (labeled d in the figure) can be computed from the Pythagorean Theorem, using the lengths of the two sides of the right triangle, r and r+h. For the geodesic (geodetic) distance (labeled g in the figure) we can use the arc cosine function, since we know two sides of the right triangle (r and r+h) and one angle (the right angle at 90 degrees). Geodesic distance is the distance over the curved surface of the earth between points O’ and P.
How far can you see if you are standing at a height of 6 ft (i.e., h=6)? At this height, the line-of-sight distance (d) and geodesic distance (g) are roughly the same at 15,837.51 ft or about 3 miles. A basketball player at 7 feet could see an extra quarter of a mile. A giraffe could see over 5 miles. A cat, only 1 mile.
Lake Michigan Example
We need to get a bit more altitude to see both shores of Lake Michigan. But we need to make a small adjustment to our calculations to account for the fact that Lake Michigan is not at sea level. The lake has an average elevation of 577.5 ft. In effect, this increases our earth radius to 20,902,809.18 ft. The giant ping-pong ball is now slightly larger than it was before.
Imagine you are flying above the lake, midway between Michigan and Wisconsin, east of Milwaukee. At this location, Lake Michigan is about 85 miles wide. To see both the Michigan and Wisconsin shorelines – assuming you had access to windows on both sides of the airplane – you need to see for a distance of 85/2 or 42.5 miles. This means you need to be at least 1,200 ft above the surface of the lake. That’s much lower than commercial airline altitudes, but also higher than the deck of the SS Badger.
Visibility Analysis in GIS
To confirm the validity of the 1,200 ft calculation, we can turn to GIS. Figure 2 was produced using ArcGIS Pro’s visibility tool. The visibility tool uses a DEM (Digital Elevation Model) to calculate the viewshed (the area that can be seen) from an observation point at a specific elevation above the surface. In this example, the DEM elevations over Lake Michigan are a constant 577.5 ft.
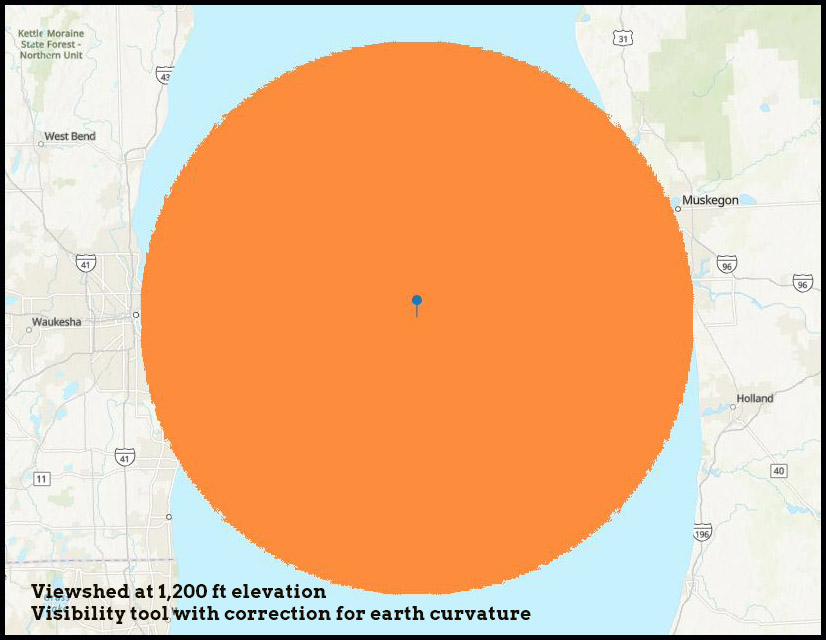
Fig. 2 – Viewshed from ArcGIS Pro at 1,200 ft
In ArcGIS Pro, there are at least three visibility tools – viewshed, visibility and geodesic viewshed. Whatever tool is chosen, users need to be aware of the significant errors that can occur if the tool does not account for the effects of earth curvature. Consider the example in Figure 3. Here we see a DEM centered on Lake Winnebago and an observer location in the middle of the lake at a height of 6 ft (2 m). Imagine you are that observer, standing up in your canoe in the middle of the lake. How far can you see? You already know the answer – about 3 miles.
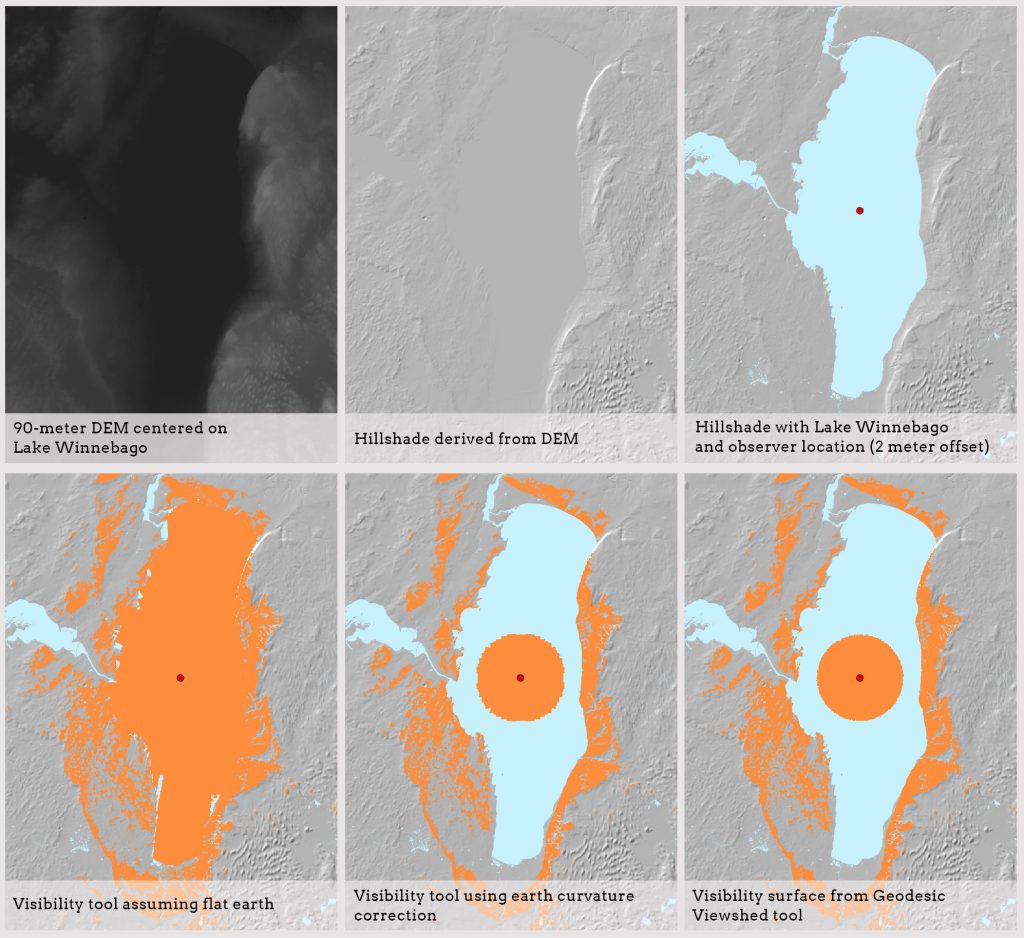
Fig. 3 – Different viewsheds based on different assumptions
However, as Figure 3 shows, running the visibility tool with the default “flat earth” assumption makes it look as if you can see the entire shoreline of the lake, from Menasha in the north to Fond du Lac in the south. But since the lake is 30 miles long north-south, we know this result is incorrect. It’s an easy mistake to make. Many users might incorrectly assume that earth curvature has a minimal effect on an area so small in size.
The other two viewsheds in Figure 3 are much better. One was created using the visibility tool with the earth curvature correction checked. The other is from the geodesic viewshed tool. The results are similar, and both viewsheds have a radius of about 3 miles. According to this document, the geodesic viewshed tool is the most accurate, since it accounts for earth’s irregular shape as an ellipsoid, while the curvature correction in the visibility tool assumes uniform curvature across the earth’s surface (i.e., a sphere).
As noted previously, all of these results are approximations based on certain assumptions, including the lack of atmospheric attenuation due to haze, dust, atmospheric diffusion of light, and so on. Some of the ArcPro tools account for refractivity using a correction factor. In reality, the distance you can see will vary from day to day depending on atmospheric conditions.
What about Francis Scott Key?
The title of this post is “O Say, Can You See?” to illustrate an easy extension of the trigonometric solution to the viewshed question. The example is historical. Just where was Francis Scott Key when he penned his famous poem during the War of 1812? History says he was on a ship close to Fort McHenry, at the mouth of Baltimore’s inner harbor, when he saw the flag gallantly streaming after a long, perilous fight. We don’t know how high the flag was. Fort McHenry is on the coast, perhaps 30 feet above the water. Let’s add another 30 feet for the flagpole. Total elevation, 60 feet. Let’s assume Key was on the deck of his ship, 20 feet above the surface of the water.
How far could Key have been from the fort and still see the flag? Was he in the thick of the fighting? Or was he possibly miles away?
Figure 4 shows the solution. We need to perform the same calculations we did in Figure 1, but for two triangles, CPO and CPQ. Point Q is the top of the flagpole at Fort McHenry. Point O is Francis Scott Key. The total line-of-sight distance is the sum of d1 and d2, while the total geodesic distance is the sum of g1 and g2. Each pair of distances converges at Point P, the horizon relative to each vantage point, O and Q.
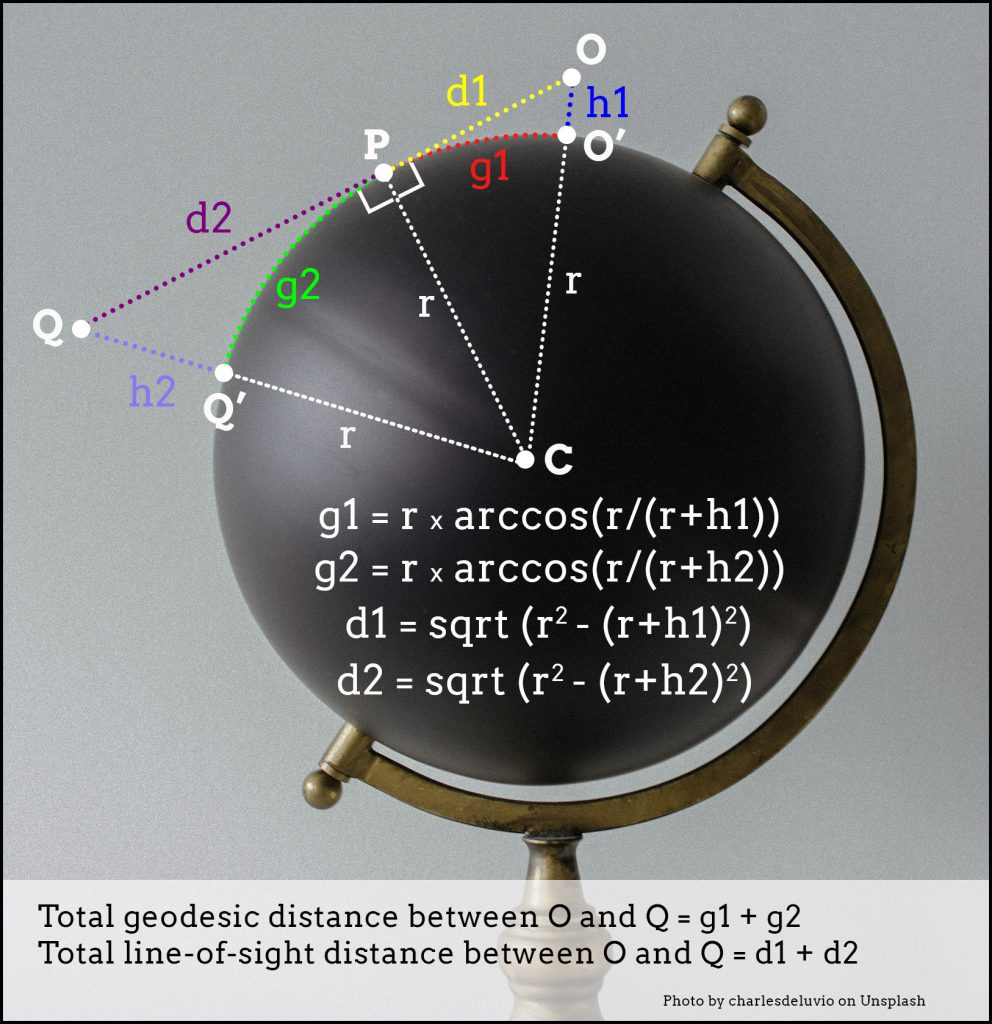
Fig. 4 – Extending the calculations
The results are in! The total geodesic distance is 15 miles. The line-of-sight distance is nearly the same. (Line-of-sight and geodesic distances start to diverge only at much higher altitudes.) In theory, then, Key could have been 15 miles away from Fort McHenry and still have seen the flag waving. He might have been in Chesapeake Bay at 39.106 deg N, 76.386 deg W, which has a clear line-of-sight over the water to the fort. Bombs bursting in air? Key might have been able to pen his famous poem without ever being in any danger!
Of course, I’m not suggesting this is what actually happened. The official story says Key was right in the thick of it, and why should we question that? The example simply demonstrates how structures of even modest height can be seen from a considerable distance. What’s true for a flagpole also applies to cell phone towers and telecommunications masts.
Comments?
I would be curious to hear from readers who have used visibility analysis in their work. What are some of the other pitfalls users need to be aware of? How much trust do you put in computed viewsheds? Please send me an email if you have comments or questions.
