You may have seen the new Apple Watch ad where the watch auto-dials 911 to relay the message that its owner has “taken a hard fall and is not responding.” The message goes on to say that “The emergency location is latitude 47.7, longitude -117.5 with an estimated search radius of 41 meters.” As a geospatial professional, do you see anything faulty in this ad?
Let’s do some rough calculations using rounded values for ease of reading. If we assume Earth is a sphere, its circumference is about 25,000 miles or 40,000 kilometers (km). (A better model of Earth’s shape is an “oblate spheroid” — an ellipsoid that slightly bulges at the equator and is slightly flattened at the poles.)
To compute the length of one degree of latitude or longitude, we need to know how many degrees there are on Earth. The answer is simple, but also a bit confusing because of the way we measure latitude and longitude.
Let’s start with latitude. There are 90 degrees of latitude between the Equator and each of the Poles. If we were to circumnavigate Earth, starting at the North Pole, then heading directly south to the South Pole, then heading north again to the North Pole, we would cover 360 degrees of latitude. This is not surprising, since the circumnavigation path would be a circle.
Furthermore, the total distance covered on our voyage would be 25,000 miles, the circumference of the spherical earth. Therefore we can easily compute that 1 degree of latitude is equal to 25,000 / 360 or 69.4 miles (111.1 km). Table 1 shows the approximate length in miles, kilometers, feet and meters for further subdivisions of a degree.
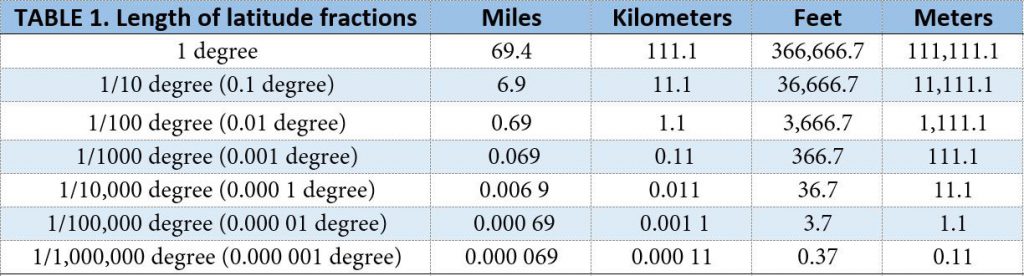
Table 1. Approximate length of fractions of a degree of latitude based on a sphere with a
circumference of 25,000 miles.
Longitude is a little trickier. There are 180 degrees of longitude in each direction, east and west, from the Prime Meridian (which is at 0 degrees longitude). These measurements meet at the meridian located at 180 East and West. The number of degrees of longitude covered if we circumnavigated Earth around the Equator would therefore be 360.
However, unlike latitude, lines of longitude converge at the poles, which means that the length of a degree of longitude is not constant. At the Equator, it will be 69.4 miles, just like latitude. But as you move north or south, the distance shrinks by a factor equal to the cosine of the latitude. Table 2 shows this relationship.
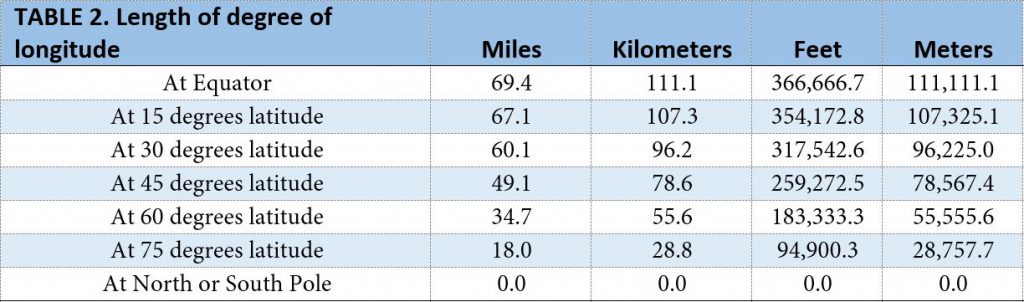
Table 2. Approximate length of a degree of longitude at different latitudes, based on a
sphere with a circumference of 25,000 miles.
For any degree of latitude, we can create a table similar to Table 1. Let’s create one for 47.7 degrees, the value used in the Apple Watch ad. (The ad doesn’t say whether it is 47.7 North or 47.7 South, but the values are the same in either case.) Table 3 shows the results.
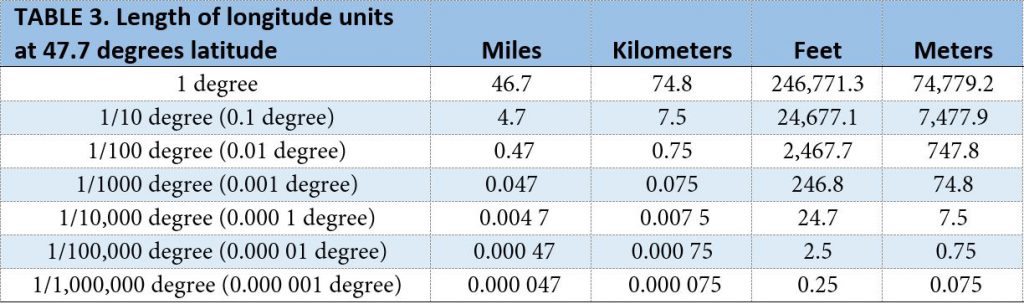
Table 3. Approximate length of fractions of a degree of longitude at a latitude of 47.7 degrees,
based on a sphere with a circumference of 25,000 miles.
In the ad, the watch relays the coordinates as 47.7 degrees latitude, -117.5 degrees longitude. These values have a precision of 1/10 of a degree. From Table 1 we see that the length of 1/10 of a degree of latitude is 6.9 miles, equivalent to 11.1 km, 36,666.7 feet, or 11,111.1 meters. For longitude, Table 3 shows us that at 47.7 degrees of latitude, the length of 1/10 of a degree of longitude is 4.7 miles, equivalent to 7.5 km, 24,677.1 feet, or 7477.9 meters.
This means that the location referenced by the watch could fall anywhere within a rectangle that extends 11,111.1 meters (6.9 miles) north-south and 7478 meters (4.7 miles) east-west.
How do we reconcile these observations with the watch’s “estimated search radius of 41 meters“? The actual search radius would be several orders of magnitude larger than this, since 1/10 of a degree — the precision of the coordinates — corresponds to thousands of meters on the ground.
The Google Earth below may help you visualize this. (This map is based on the assumption that the location in the ad is 47.7 degrees North, not 47.7 degrees South.) The search area, given coordinates with 1/10 degree precision, is approximated by the yellow rectangle. The rectangle is shorter east-west than north-south because of the convergence of lines of longitude (as explained above) but it’s still a big, big area. The “41 meter” search radius is so small that it cannot really be seen on map of this scale.
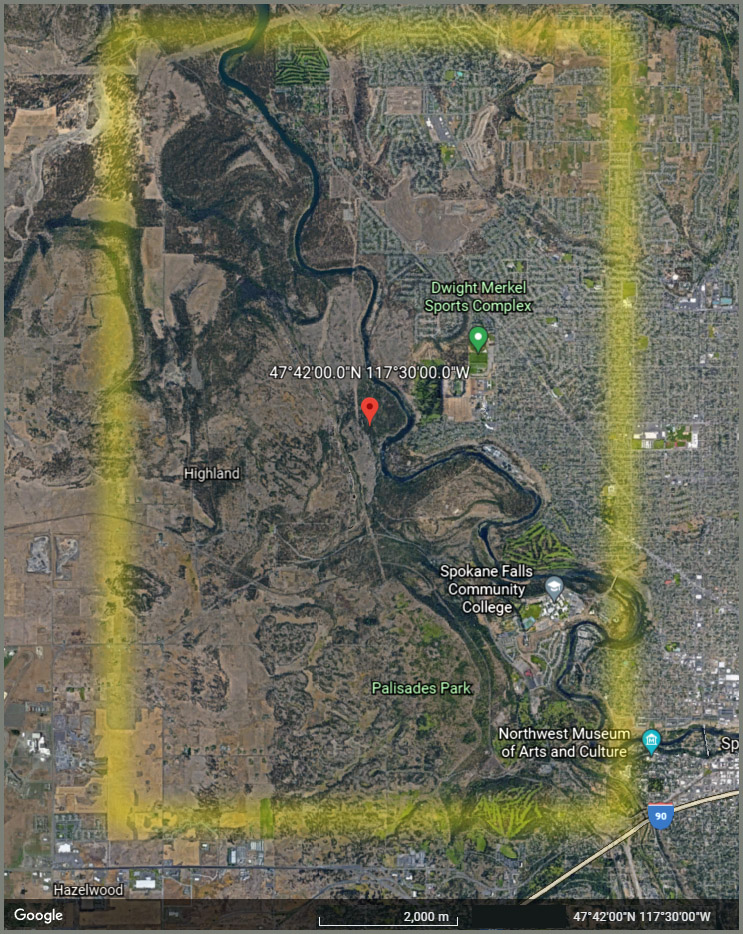
Google Earth map showing the approximate rectangle corresponding to 47.7 degrees latitude, -117.5 degrees longitude.
Does this mean there’s no hope of being found if you rely on your Apple Watch to rescue you? Probably not. I suspect that Apple is simply “dumbing down” its ad so that consumers are not confronted with coordinates with four numbers after the decimal place, which is the precision needed to get down to tens of meters in length.
But it doesn’t hurt to question what you see, especially when it touches on an area of expertise most of you will identify with. Next time you see the ad, ask your spouse or your kids if they see anything wrong with it, and help them be better educated consumers and geographers!
