In an earlier post, I challenged readers to find a solution to a cartographic problem: What is the latitudinal deviation (at a chosen meridian) between a given parallel (a line of latitude) and a great circle arc tangent to that parallel at a given point, where the great circle is the projection of a line heading east on a compass.
Recall (from the earlier post) that all parallels bear the same angular relationship to every meridian, along the entire length of the parallel. In other words, at every point on the parallel, the curve bears due east and west.
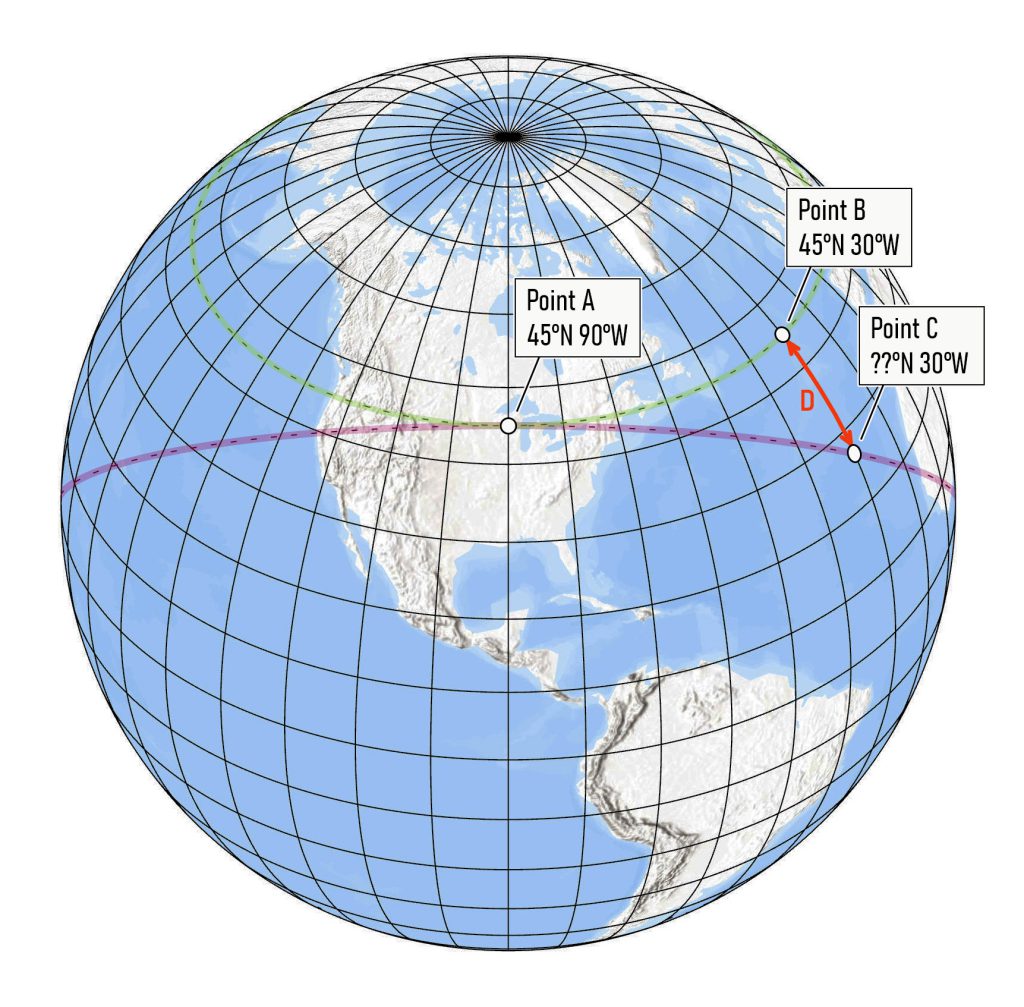
The green dashed line in Figure 1 is an example for the parallel at 45 degrees North. In other words, the green line describes a true east-west line. If you started at Point A and followed the green line, you would maintain the same angular relationship to north (i.e., 90 degrees).
On the other hand, if you placed a compass at Point A with the arrow pointing north, the projection of the imaginary line pointing east on the compass would follow a much different path. This line would describe a great circle of the earth gradually departing southerly from the true parallel. This is shown in Figure 1 by the pink dashed line.
Fig 1. The earth’s graticule, with an illustration of the problem
Your challenge was to find the distance D along the meridian at 30 degrees W. The value of 30 has no special significance. It is just an example.
Unfortunately, I did not receive any responses to the challenge! Nevertheless, I have developed a solution, which I share below.
A Solution
There are several ways to solve this problem. My approach is based on solving spherical triangles using trigonometric rules that have analogs in more conventional Euclidean geometry. (This turned out to be easier than I expected, given that I have no background in spherical trigonometry.) The key to solving the problem is to define a set of spherical triangles (triangles whose sides are formed by great circle arcs) for which we know at least three of the six angles and sides. With those three pieces of information, the unknown angles and sides can be computed. One other thing to note about spherical triangles is that their sides can be expressed as angles, since they are arcs of great circles that subtend an angle at the center of the sphere.
Figure 2 shows the calculations involved to find the latitude of Point C and the length of arc D. Points A, B and C are the same as on Figure 1. Point E is a new point located on the Equator 90 degrees east of Point A. Point E is on the great circle arc shared with Points A and C. For any point at any latitude, the great circle arc heading east from that point will intersect the Equator at a point 90 degrees to the east.
Fig 2. Details on the solution
Since Point E has known latitude and longitude (0 degrees N and 0 degrees W in our example), we can use it to construct a spherical triangle with vertices at Point A, the North Pole, and Point E. For this triangle, we know the length (angle) of Arc P connecting Point A to the North Pole, the length (angle) of Arc R connecting Point E to the North Pole, and Angle v between Arcs P and R. (The angle is 90 degrees by definition.)
We can use these values to compute Angle z, the angle formed between Arc R and the great circle arc. The equation to compute Angle z is shown in Figure 2.
Given Angle z, we now have the three pieces of information (Angle z, Angle x, and Arc R) we need to compute Angle y, the angle formed between the great circle arc and Arc Q (connecting Point C to the North Pole). The equation for Angle y is shown in Figure 2.
Given Angle y, we can now compute the length (angle) of Arc Q based on Angles x, y and z. This gives us the latitude of Point C, which leads to the latitudinal difference between Points B and C, which is the angle represented by Arc D. We can now compute the length of Arc D.
The length is approximately 2052.17 km. So, if you followed the projected direction from your compass, thinking you were going east, you would be over 2000 km off-course after travelling 60 degrees east.
Notes on Precision and Calculations
Given that we are already generalizing angles and distances by relying on a spherical earth model, we should not expect too much precision in the results. To keep the precision of distances (in km) somewhere between 1 km and 1 m, I use 2 decimal places for distances. This implies about 4 decimal places for coordinates in decimal degrees, and about 6 decimal places for angles expressed as radians.
All calculations are done on a sphere of unit radius. For the final calculation of the length of Arc D, a radius of 6378 km is used, which translates into 111.32 km per degree. All calculations are done in radians since most trigonometric functions in software expect inputs in radians, not degrees.
Note also that there may be rounding errors in the return values of trigonometric functions, depending on which software is used and the defined precision of floating point numbers.
Extension to Other Locations
Obviously, Point A is just one of an infinite number of points that could be selected as an example. The solution described here will generally work with any location, subject to some caveats.
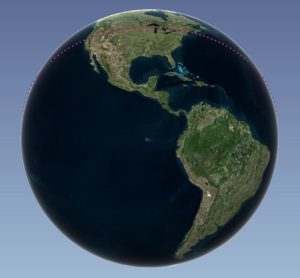
First, the deviation between Points B and C only needs to be computed for a 90-degree wedge to the east of Point A, wherever Point A might be located. The pattern of deviations simply repeats itself in a mirror image as you move around the earth. You can see this in the visualization below, which shows the trace of the great circle passing through Point A. In other words, it shows the location of Point C as this point moves around the earth given different longitudinal values. (Incidentally, this visualization was created in Microsoft Excel. Did you know that Excel provides basic mapping tools?)
Fig. 3. Click to view visualization
The equations will not work without modification if Point A is in the southern hemisphere, but the values for the southern hemisphere are just mirror images of those in the northern hemisphere, so the equations can still be used with slight modifications.
A problem will also occur if Point A and Point E are on opposite sides of 180 degrees East/West. In this case, a solution would be to transform the negative longitude values into positive longitudes ranging from 0 degrees at the Prime Meridian to 360 degrees as you move east around the globe.
Confirmation of Results
Can we be sure the results are accurate? To confirm the results, I compared them to those obtained by another method, described here by Dr. Louis Strous. His example #4 (“A Great Circle in a Certain Direction Through a Known Point”) involves converting latitude and longitude to 3-dimensional Cartesian coordinates (x, y, z) and then computing the location of a point at a known distance from a starting point traveling in a known direction. I adapted this method to our problem by simplifying it to account for the fact that we are always traveling in an easterly direction. I used the Solver in Excel to find the latitude of Point C by iteratively changing the distance value until a solution was obtained. Aside from rounding error, results are identical to the method described above.
Acknowledgements
Thanks to Mike Hasinoff for checking my math and being interested in the problem, Dr. Louis Strous for his inspiration, and this Wikipedia page.