Which way is east? The answer to this question may seem simple enough. After all, we all know that east is at a right angle (90 degrees) to north. All you need to do is look at a compass.
But, it turns out, the answer is more complicated than that.
For the purposes of this discussion, I first want to put aside the question, “Which way is north?” There are several definitions of north, including geodetic north (based on the rotational axis of the earth), the approximation of celestial north based on the north star (Polaris), magnetic north (defined by the earth’s magnetic field), grid north (direction of the grid system on a map), as well as the (often incorrect) north arrows seen on maps that point “up” despite the convergence of meridians on the map itself.
This is an important topic, but not the subject of this blog post. Regardless of the exact definition of north, the arguments I make in this post remain basically the same.
It’s complicated!
What makes east (and west too) tricky is the earth’s curvature. (Note: This discussion assumes a perfectly spherical earth to avoid complications that do not affect the main points being made.) Remember that, looking at our compass, east is 90 degrees clockwise from north. Now consider the earth’s graticule, the network of lines of latitude and longitude covering the earth. See Figure 1 below.
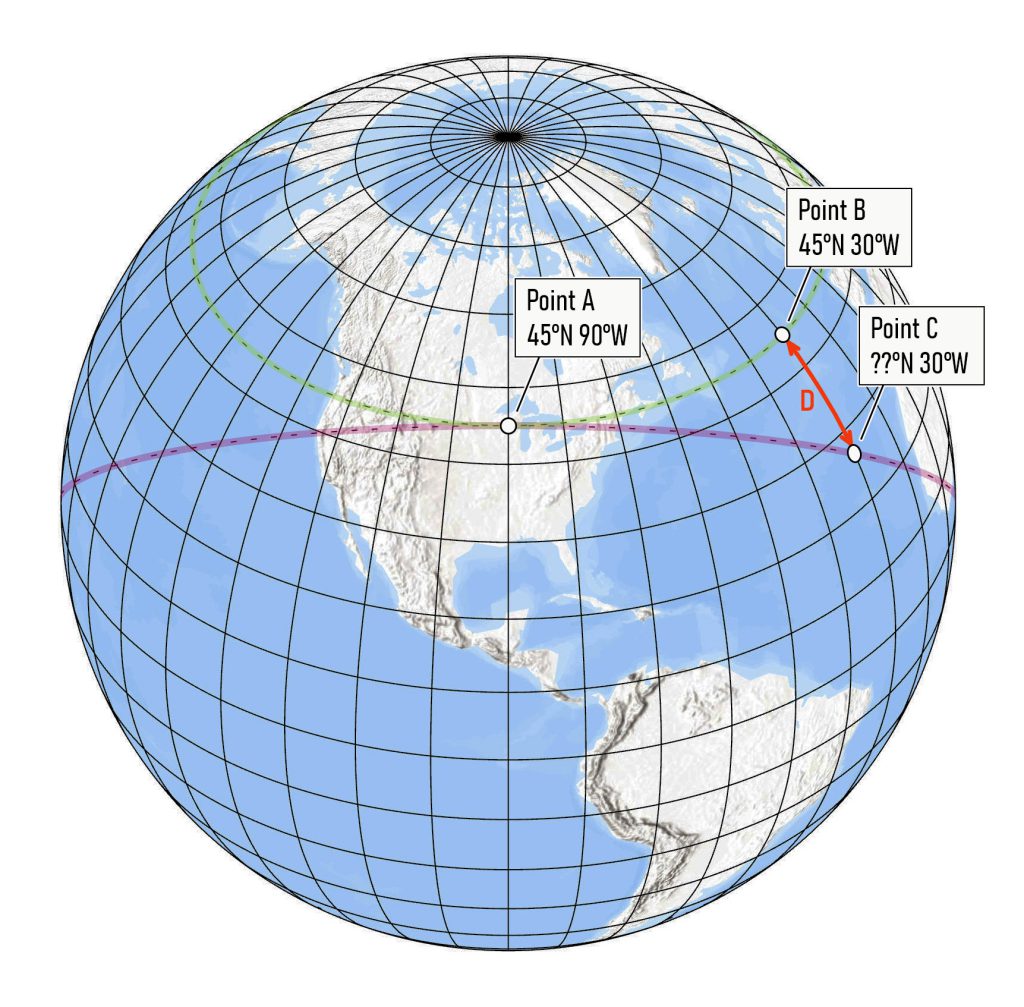
Fig 1. The earth’s graticule, with an illustration of the problem
We know that meridians (lines of longitude) are north-south lines connecting the North and South Poles. (Note: I will use the term “line” here even though these features are obviously curves. Nobody calls meridians “curves of longitude” after all.)
We can see that all parallels (lines of latitude) bear the same angular relationship to every meridian, along the entire length of the parallel. The following quotation from the Bureau of Land Management’s “Manual of Surveying Instructions” (1973, p. 53) says it best,
At every point on the true parallel, the curve bears due east and west, the direction of the the line being at right angles to the meridian at every point along the line.
This means that every parallel is a “rhumb line” or “loxodrome” — a line of constant bearing.
The green dashed line in Figure 1 is an example for the parallel at 45 degrees North. In other words, the green line describes a true east-west line. If you started at Point A and followed the green line, you would maintain the same angular relationship to north (i.e., 90 degrees).
On the other hand, if you placed a compass at Point A with the arrow pointing north, the projection of the imaginary line pointing east on the compass would follow a much different path. Quoting again from the “Manual of Surveying Instructions” (p. 53),
…the projection of a line so defined in either direction, easterly or westerly, would describe a great circle of the earth gradually departing southerly from the true parallel.
The great circle arc is shown as the pink dashed line in Figure 1. (Note: a great circle divides the spherical earth in two equal halves.) This is the path you would follow if you used the compass direction you observed at Point A, and then set out in that direction.
This should make you rethink the accuracy of the old saying, “East is East and West is West.” (Actually this is from a Rudyard Kipling poem, in a very different context.)
How big a deal is this?
In Figure 1, the pink great circle arc is tangent to the green parallel only at Point A. At this point and this point only, the two lines are both at 90 degrees from north. In contrast to the parallel, the great circle arc does not have the same angular relationship to north along its entire length. You can see that the angle increases as you move away from Point A along the arc. The arc no longer heads east, but rather southeast. It reaches its maximum angle at 90 degrees of longitude from Point A, at which point the angle slowly returns to 90.
The change in the angle depends on the distance from the point of tangency (Point A). Also, the rate of change in the angle depends on the latitude of the point of tangency.
The question is, how much of a difference would this make if you were trying to, say, draw a curve on the earth corresponding to a parallel. Obviously, if you were close to the point of tangency, it might make very little difference, but further away, the deviation would become larger. In Figure 1, you can see that at 30 degrees West (60 degrees of longitude from Point A), the deviation between the parallel and the great circle arc is quite large, as shown by the red arrow marked D.
The reason this is covered in the “Manual of Surveying Instructions” is because, when the Public Land Survey System was created, surveyors often needed to survey a parallel of latitude (the Illinois-Wisconsin boundary is an example) in less-than-ideal conditions. The so-called “tangent method” to determine a true latitude line (i.e., a parallel) is based on the projection of the easterly line from the initial point of tangency. A correction factor is then used to shift locations from the resulting great circle arc back to the parallel. Details, however, are given in chains (rather than feet or meters) and the correction factor is not explained in detail. Figures 2 and 3 are taken from the 1973 edition of the manual.
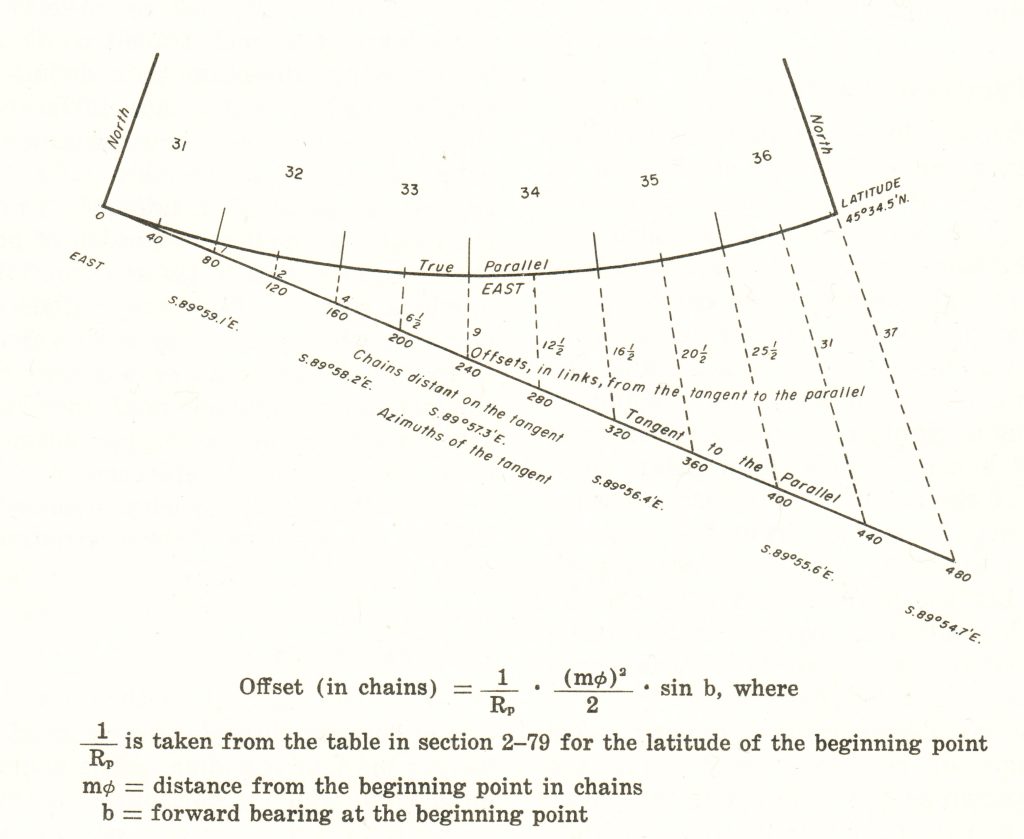
Fig 2. Figure 13 from p. 54 of the 1973 edition of Manual of Surveying Instructions. The feature labeled “Tangent to the Parallel” is a great circle arc.
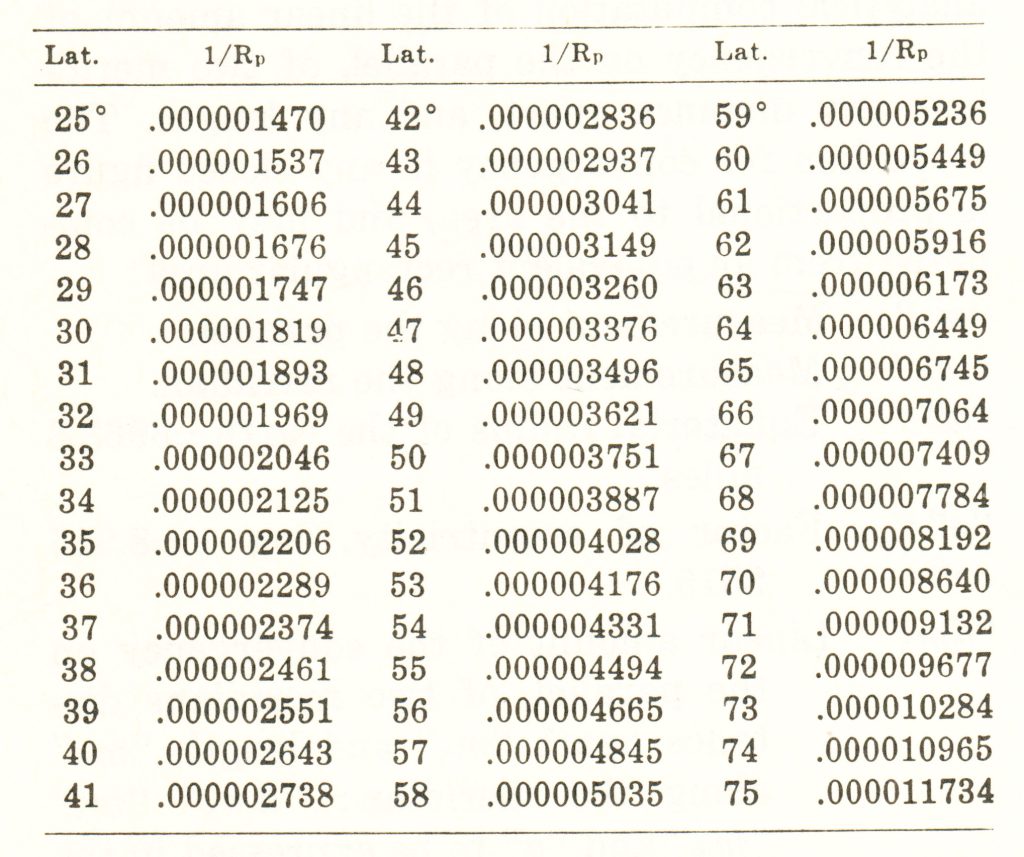
Fig 3. Table in section 2-79, p. 56 of the 1973 edition of Manual of Surveying Instructions
What is the reader challenge?
Your challenge, if you choose to accept it, is to determine the equations that can be used to compute the deviation (D) along a meridian between a parallel and a great circle arc tangent to that parallel at a point. An example is shown by the red arrow labeled D in Figure 1. However, your method must be general enough to use for a) any parallel and b) any meridian.
Remember that there are an infinite number of great circle arcs for any point. The one you need is the one for which D is equal at the same angular distance east and west of the point of tangency.
Think you know the answer? Send us an email! I’ll announce results after giving some time to collect responses. Please try to get your responses in by May 31, 2024.
To be clear, I do not know the answer. I’m hoping a professional (or aspiring) surveyor, geodesist or cartographer out there takes and interest in this esoteric (but important) question and solves it!
